Entropic Evaluation of Classification
A hands-on, get-dirty introduction

Sunday, 8 July 2018, Oceania 7

Resources

Slides for IJCNN-04 tutorial: IJCNN18-EntropyTriangle

Implementations of the Entropy Triangle:

R Package and an initialisation file to configure the libraries dependencies.
Weka package
Matlab package
Python package: to be released soon.

Use case vignettes in R

If you really want to get dirty, these are the use cases we will use to illustrate the affordances of the Entropy Triangle in Rmd: Analysis of Confusion Matrices and Simple Use Case for the CBET on classification. You will be able to analyse different classifiers and find out yourself what the Entropy Triangle is doing. In this case, it is recommended to have R Studio installed.

For those who just want to peruse the illustration cases: Analysis of Confusion Matrices and Simple Use Case for the CBET on classification

Our project in ResearchGate:

Web page at ResearchGate where updates to it are posted:

https://www.researchgate.net/project/Evaluation-of-Machine-Learning-Techniques-by-Entropic-Means

The main papers for the theory:

The first introduction to the Entropy Triangle CBET [1] and related metrics EMA \& NIT [2], the source multivariate extension SMET [3] and the channel multivariate extension CMET [4].

[1]

Francisco~J.~Valverde-Albacete and C. Peláez-Moreno, “Two information-theoretic tools to assess the performance of multi-class classifiers,” Pattern Recognition Letters, vol. 31, iss. 12, pp. 1665-1671, 2010.
[Bibtex]

@article{val:pel:10b,
  Doi = {10.1016/j.patrec.2010.05.017},
  Author = {Francisco~J.~Valverde-Albacete and Carmen Pel\'aez-Moreno},
  Date-Added = {2016-02-11 13:49:50 +0000},
  Date-Modified = {2016-02-11 13:49:50 +0000},
  Journal = {Pattern Recognition Letters},
  Number = {12},
  Pages = {1665--1671},
  Title = {Two information-theoretic tools to assess the performance of multi-class classifiers},
  Volume = {31},
  Year = {2010}}

[2]

F. J.~Valverde-Albacete and C. Peláez-Moreno, “100\% classification accuracy considered harmful: the normalized information transfer factor explains the accuracy paradox,” PLOS ONE, pp. 1-10, 2014.
[Bibtex]

@article{val:pel:14a,
  Author = {Francisco J.~Valverde-Albacete and Carmen Pel\'aez-Moreno},
  Date-Added = {2016-02-11 13:49:37 +0000},
  Date-Modified = {2016-02-11 13:49:37 +0000},
  Doi = {10.1371/journal.pone.0084217},
  Journal = {PLOS ONE},
  Month = {january},
  Pages = {1--10},
  Title = {100\% classification accuracy considered harmful: the normalized information transfer factor explains the accuracy paradox},
  Year = {2014},
  Bdsk-Url-1 = {http://dx.doi.org/10.1371/journal.pone.0084217}}

[3]

F. J. Valverde-Albacete and C. Peláez-Moreno, “The Evaluation of Data Sources using Multivariate Entropy Tools,” Expert Systems with Applications, vol. 78, pp. 145-157, 2017.
[Bibtex]

@article{val:pel:17b,
  Author = {Valverde-Albacete, Francisco J and Pel\'aez-Moreno, C},
  Date-Added = {2017-03-02 10:57:06 +0000},
  Date-Modified = {2017-03-02 10:57:06 +0000},
  Doi = {10.1016/j.eswa.2017.02.010},
  Journal = {Expert Systems with Applications},
  Pages = {145-157},
  Title = {The Evaluation of Data Sources using Multivariate Entropy Tools},
  Volume = {78},
  Year = {2017},
  Bdsk-Url-1 = {http://dx.doi.org/10.1016/j.eswa.2017.02.010}}

[4]

F. J. Valverde-Albacete and C. Peláez-Moreno, “Assessing Information Transmission in Data Transformations with the Channel Multivariate Entropy Triangle,” Entropy, vol. 20, iss. 7, 2018.
[Bibtex]

@article{val:pel:18c,
AUTHOR = {Valverde-Albacete, Francisco J. and Pel\'aez-Moreno, Carmen},
TITLE = {Assessing Information Transmission in Data Transformations with the Channel Multivariate Entropy Triangle},
JOURNAL = {Entropy},
VOLUME = {20},
YEAR = {2018},
NUMBER = {7},
Doi = {10.3390/e20070498},
ISSN = {1099-4300},
ABSTRACT = {Data transformation, e.g., feature transformation and selection, is an integral part of any machine learning procedure. In this paper, we introduce an information-theoretic model and tools to assess the quality of data transformations in machine learning tasks. In an unsupervised fashion, we analyze the transformation of a discrete, multivariate source of information X¯ into a discrete, multivariate sink of information Y¯ related by a distribution PX¯Y¯. The first contribution is a decomposition of the maximal potential entropy of (X¯,Y¯), which we call a balance equation, into its (a) non-transferable, (b) transferable, but not transferred, and (c) transferred parts. Such balance equations can be represented in (de Finetti) entropy diagrams, our second set of contributions. The most important of these, the aggregate channel multivariate entropy triangle, is a visual exploratory tool to assess the effectiveness of multivariate data transformations in transferring information from input to output variables. We also show how these decomposition and balance equations also apply to the entropies of X¯ and Y¯, respectively, and generate entropy triangles for them. As an example, we present the application of these tools to the assessment of information transfer efficiency for Principal Component Analysis and Independent Component Analysis as unsupervised feature transformation and selection procedures in supervised classification tasks.}
}

Organizers

Francisco J. Valverde-Albacete

Departamento de Teoría de la Señal y de las Comunicaciones
Universidad Carlos III de Madrid
Avda de la Universidad, 30. Leganés 28911 (España)
https://www.researchgate.net/profile/Francisco_J_Valverde-Albacete

Carmen Peláez-Moreno

Departamento de Teoría de la Señal y de las Comunicaciones
Universidad Carlos III de Madrid
Avda de la Universidad, 30. Leganés 28911 (España)
https://www.researchgate.net/profile/Carmen_Pelaez-Moreno

Description of Goal

To evaluate supervised classification tasks we have two different data sources:

The observation vectors themselves to be used to infer the classifier to obtain the predicted labels.
The true labels of the observations to be compared to the predicted labels in the form of a confusion matrix

Two main kinds of measures try to analyze the confusion matrix: count-based measures (accuracy, TPR, FPR and derived measures, like AUC, etc.) and entropy-based measures (variation of information, KL-divergence, mutual information and derived measures).

The first kind use the minimization of such error count-based measures as heuristic to improve the quality of the classifier, while the latter try to optimize the flow of information between input and output label distributions (e.g. minimize variation of information, maximize mutual information).

Specifically, this second type of evaluation considers the classification an information-transmitting channel like the one seen in Figure 1 where K are the labels, X the observation vectors, Y a possible transformation of the observations, and $\hat K$ , the predicted labels.

Figure 1: Conceptual scheme for the measurement of the information balances in a
multiclass/multilabel classification task.

The purpose of the tutorial is to train attendees in using a visual and numerical standalone tool, the Entropy Triangle, to carry out entropy-based evaluation on the blocks of Figure 1 and how to compare it to accuracy-based evaluation.

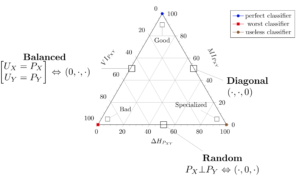
This is schematically shown in Figure 2 where an entropy triangle is shown for a joint distribution P_XY.

Figure 2:
Schematic ET as applied to supervised classifier assessment (from [1])

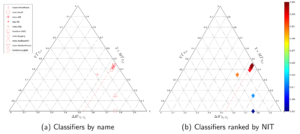
The idea is to apply this triangle on the distribution of true and predicted labels issued from the classifier $P_{K\hat{K}$ . Every single classifier, evaluated on its confusion matrix appears as a distinct dot in the previous diagram and has different characteristics depending on whether it is closer to each of the apexes. For instance, the triangles in Figure 3 show how
different classifiers in WEKA can be evaluated on the same task—in this case anneal from the UCI repository—, a diagram that is relevant for data challenge competitions on supervised classification.

Figure 3: (Color online) Entropy triangle for some Weka classifiers on the UCI anneal task

We will also offer a glimpse on how Entropy Triangles can be used

to ascertain whether the underlying classification task, that is the labels and the observations (K,X) is easy to solve or not, and
even if the transformed features Y are going to be good or detrimental to the process.

Learning by doing

Axiomatic approaches to evaluation ([2, 3]) sometimes forget that the proof of the pudding is in the eating. We intend to entreat attendees to bring their own confusion matrices and cook some good entropy triangles with them. We will guide attendants along a session where they will learn to assess a single classifier, then compare different classifiers in the same task and finally evaluate a classifier in different
tasks.

When the data challenges for IJCNN’18 are decided and if any of them is a classification task, we intend to contact the challenge organizers so that we can analyze the data in the tutorial along with the attendants.

The main expected outcome of the tutorial is that when attendants see a classifier evaluated on a dataset and represented in an Entropy Triangle they will be able to judge what is wrong or right with it: whether the data are
unbalanced, whether the classifier is good on the dataset or whether it is over-trained, etc.

And, perhaps more importantly, we will advise them on when to trust and when not to trust accuracy without p-values! ([1]).

The entropy triangle is available in this basic configuration for Matlab, R and Weka. It is also forthcoming for Python, and these resources will be made available to the attendants.

Plan of the session

The following points will be roughly evenly distributed in the 2h for the tutorial

Intro: multi-class classification assessment and confusion matrices. We will extend the material in the introduction above.
The entropy balance equation and the entropy triangle. We will introduce this visualization technique that acts as a visual summary of the normalized variation of information, mutual information and divergence from uniformity, of a joint distribution.
Assessing single classifiers with the ET. At first, we will provide simple guidance on how to assess individually sampled confusion matrices. When to say on absolute terms that a classifier is good, bad or it is cheating (on some data).
Assessing a type of classifier on several tasks with the ET. We will show attendees how they can visualize the “no free lunch theorem” on their own classifiers to prevent public remonstrance at conferences.
Assessing several types of classifiers on the same task with the ET. We will use this modality to carry out task assessment at a glance. We will get dirty with data and see examples of when a task has not been solved by a community in spite of stating accuracies of 65% and above.
Assessing a data source with a variation of the ET. We will use this modality to see if the data is unbalanced or if the transformed features Y are good.

Outline of the Covered Material

The traditional distinction between classification measures roughly parallels the error-counting vs. the entropy-summing distinction: the first uses techniques from classical statistics, while the second uses classical information theory [4, 5]).

In this view, the confusion matrix is a summary of the errors and successes of the classifier in the test data. For binary classification tasks, the measure of success is accuracy and the measures of errors are the False Positive Rate (FPR) and False Negative Rate (FNR). If the classifier-inducing technique has any parameters, the balance of FPR vs FNR as parameterised can be observed in the ROC curve ([6]). If a single measure is required, the Area-Under-the-Curve is a convenient summary of it ([7]). Although accuracy is straightforwar for more than two classes, the multi-class ROC and Volume-Under-the-Curve took longer to be generalised. FPR and FNR are not used in this context.

Are so many measures necessary? The paramount error-counting measure, accuracy, is known to suffer from a paradox: good lab measurements often drop spectacularly on deployment ([8]), among other problems ([9]). Yet it is the measure most often reported for classifiers.

The model behind entropy measurements is that a classifier is a channel of information from the data to the output class labels (see Figure 1): the better this channel is, the better the classifier has captured the “essence” of the task and hence, the more interpretable the results are. In this sense, the confusion matrix is the joint distribution between input and output channels. Of course this second interpretation is added on top of the previous one.

In this interpretation, the variation of information ([10]) measures how different the set of input and output labels are: this is a quantity to be minimized. Similarly, the mutual information (MI) ([11]) measures how similar both sets are, so this is a quantity to be maximized. Note that since MI is just the Kullback-Leibler divergence between the joint distribution of input and output labels and their marginals, many intuitions regarding the KL-divergence can be applied to MI.

In this picture, the actual entropy on the input labels has great importance since it provides limits to the amount of information that classifiers can learn from the training data: maxims like “the processing of information can only deteriorate it” depend on this. Many measures try to include this factor by normalizing wrt marginal entropies.

An analogue of the ROC in this context is the Entropy Triangle (ET) ([12]) (see Figure 2), showing the balance of MI, VI and entropies of the marginals. Likewise, a summary measure on the ET is the Entropy-Modified Accuracy (EMA) ([1]), and it goes hand in hand with the Normalized Information Transfer rate, measuring the actual fraction of information learnt by a classifier.

In this tutorial we present a new context for entropic measures and introduce the attendees to an entropy-based visualization aid to evaluate multi-class classifiers stemming from their confusion matrices. At the beginning we make explicit the information theoretic model for confusion matrices ([11]) and provide easy-to-understand information-theoretic introduction to the Entropy Triangle which is capable of balancing mutual information and the variation of information and, at the same time take into consideration the peculiarities of datasets.

Since it is difficult for an practitioner not to come up with her own measure, we provide a glimpse into the affordances of Entropy-Modulated Accuracy and Normalized Information Transfer rate ([1]) for measuring performance and learning ability, respectively.

This basic framework can be extended to data source evaluation?, and to the evaluation of multivariate data transformations?. However, these are advanced topics and will only be dwelt upon if the attendants demand further information.

This research line has a Web page at ResearchGate where updates to it are posted:

https://www.researchgate.net/project/Evaluation-of-Machine-Learning-Techniques-by-Entropic-Means

Justification

This tutorial is intended for practitioners in machine learning and data science who have ever been baffled by the evaluation of their favorite pet classifier. Since the technique is technology-agnostic it can be used in any form of classifier and supervised classification data whatsoever (and indeed for many more type of datasets!).

The not-so-gory details are easy to understand to researchers and students who have ever seen and understood the concepts of entropy, mutual information and Venn-diagrams.

We are aiming at a 1.5h duration to develop the learning outcomes spelled above. But we could extend it to 3h if necessary and include more examples of evaluation, more in-depth analysis, and a bit of theoretical justification after the main ideas were captured in learning to read the visual tool.

Information-theoretic methods of evaluation are being actively pursued to justify e.g. the good results of deep learning with success [13, 14]. This tutorial address this issue from an technique-independent, wide scope that will help attendants apply it to their own experiments and research. These aims are furthered by the ready-to-use SW that attendants will be acquainted with.

Although this is the first time this tutorial will be taught, the authors have explained this material in research talks at several groups, Ph.D. classes and conferences for the past 5 years.

They have a tendency to explain it to solitary researchers too much unawares of what is about to befall them. They unanimously get open eyes and mouths from older researchers and expressions of ”So what?” from younger ones. There have been 2 journal papers (PLOS ONE, Pattern recognition letters) and 2 conference papers (Interspeech, CLEF) written around this topic.

Francisco J. Valverde-Albacete has been teaching a number of subjects in Electrical Engineering, Signal processing, data mining and pattern recognition for the past 20+ years, including master and Ph.D. level subjects. His interests now lay in Information Theoretic approaches to Machine Learning and non-standard algebras for signal processing.

Carmen Peláez-Moreno has been teaching a number of subjects in Signal Processing, Speech, Audio and Multimedia processing and Pattern Recognition for the past 20+ years, including master and Ph.D. level subjects. She is an Associate Professor in the Multimedia Processing group at Universidad Carlos III de Madrid, Spain, where she applies signal processing to Automatic Speech Recognition.

Special requirements

Internet connection, participants should bring their computers with Octave (Matlab), R, Python
and/or Weka installed.

References

[1]

F. J.~Valverde-Albacete and C. Peláez-Moreno, “100% classification accuracy considered harmful: the normalized information transfer factor explains the accuracy paradox,” PLOS ONE, vol. 9, iss. 1, pp. 1-10, 2014.
[Bibtex]

@article{val:pel:14a,
  Author = {Francisco J.~Valverde-Albacete and Carmen Pel\'aez-Moreno},
  Date-Added = {2014-03-07 20:08:11 +0000},
  Date-Modified = {2014-03-07 20:08:11 +0000},
  Doi = {10.1371/journal.pone.0084217},
  Journal = {PLOS ONE},
  Month = {January, 10},
  Number = {1},
  Pages = {1-10},
  Title = {100% classification accuracy considered harmful: the normalized information transfer factor explains the accuracy paradox},
  Volume = {9},
  Year = {2014},
  Bdsk-Url-1 = {http://dx.doi.org/10.1371/journal.pone.0084217}}

[2]

M. Sokolova and G. Lapalme, “A systematic analysis of performance measures for classification tasks,” Information Processing & Management, vol. 45, iss. 4, pp. 427-437, 2009.
[Bibtex]

@article{sok:lap:09,
  Author = {Marina Sokolova and Guy Lapalme},
  Date-Added = {2014-03-07 20:08:02 +0000},
  Date-Modified = {2014-03-07 20:08:02 +0000},
  Doi = {10.1016/j.ipm.2009.03.002},
  Journal = {Information Processing {\&} Management},
  Local-Url = {file://localhost/Users/fva/Documents/Papers/2009/Sokolova/Sokolova%202009%20A%20systematic%20analysis%20of%20performance.pdf},
  Month = {Jul},
  Number = {4},
  Pages = {427--437},
  Pii = {S0306457309000259},
  Rating = {0},
  Title = {A systematic analysis of performance measures for classification tasks},
  Uri = {papers://15492FEA-4C5B-4BEA-89B8-8663EEC734AB/Paper/p18388},
  Volume = {45},
  Year = {2009},
  Bdsk-File-1 = {YnBsaXN0MDDUAQIDBAUGJCVYJHZlcnNpb25YJG9iamVjdHNZJGFyY2hpdmVyVCR0b3ASAAGGoKgHCBMUFRYaIVUkbnVsbNMJCgsMDxJXTlMua2V5c1pOUy5vYmplY3RzViRjbGFzc6INDoACgAOiEBGABIAFgAdccmVsYXRpdmVQYXRoWWFsaWFzRGF0YV8QYS4uLy4uLy4uLy4uL0RvY3VtZW50cy9QYXBlcnMvMjAwOS9Tb2tvbG92YS9Tb2tvbG92YSAyMDA5IEEgc3lzdGVtYXRpYyBhbmFseXNpcyBvZiBwZXJmb3JtYW5jZS5wZGbSFwsYGVdOUy5kYXRhTxEDZAAAAAADZAACAAADZnZhAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAx01OV0grAAUAAnDgH1Nva29sb3ZhIDIwMDkgQSBzeXN0IzM2MUE0RS5wZGYAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA2Gk7GlO10UERGIENBUk8ABAAFAAANAgAAAAAAAAAAAAAAAAAAAAhTb2tvbG92YQAQAAgAAMdNQEcAAAARAAgAAMaU0VQAAAABABAAAnDgAAJwpgACaq8AAmmmAAIAQmZ2YTpEb2N1bWVudHM6UGFwZXJzOjIwMDk6U29rb2xvdmE6U29rb2xvdmEgMjAwOSBBIHN5c3QjMzYxQTRFLnBkZgAOAG4ANgBTAG8AawBvAGwAbwB2AGEAIAAyADAAMAA5ACAAQQAgAHMAeQBzAHQAZQBtAGEAdABpAGMAIABhAG4AYQBsAHkAcwBpAHMAIABvAGYAIABwAGUAcgBmAG8AcgBtAGEAbgBjAGUALgBwAGQAZgAPAAgAAwBmAHYAYQASAFYvRG9jdW1lbnRzL1BhcGVycy8yMDA5L1Nva29sb3ZhL1Nva29sb3ZhIDIwMDkgQSBzeXN0ZW1hdGljIGFuYWx5c2lzIG9mIHBlcmZvcm1hbmNlLnBkZgATAAovVXNlcnMvZnZhABQBXAAAAAABXAACAAEMTWFjaW50b3NoIEhEAAAAAAAAAAAAAAAAAAAAxquYFkgrAAAAB/whEGZ2YS5zcGFyc2VidW5kbGUAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAH/CK2dYdYAAAAAAAAAAD/////AAAJIAAAAAAAAAAAAAAAAAAAAAQuZnZhABAACAAAxqt79gAAABEACAAAtnV5SAAAAAEACAAH/CEAAJDnAAIAKE1hY2ludG9zaCBIRDpVc2VyczouZnZhOmZ2YS5zcGFyc2VidW5kbGUADgAiABAAZgB2AGEALgBzAHAAYQByAHMAZQBiAHUAbgBkAGwAZQAPABoADABNAGEAYwBpAG4AdABvAHMAaAAgAEgARAASABtVc2Vycy8uZnZhL2Z2YS5zcGFyc2VidW5kbGUAABMAAS8A//8AAAAVAAIACv//AACABtIbHB0eWiRjbGFzc25hbWVYJGNsYXNzZXNdTlNNdXRhYmxlRGF0YaMdHyBWTlNEYXRhWE5TT2JqZWN00hscIiNcTlNEaWN0aW9uYXJ5oiIgXxAPTlNLZXllZEFyY2hpdmVy0SYnVHJvb3SAAQAIABEAGgAjAC0AMgA3AEAARgBNAFUAYABnAGoAbABuAHEAcwB1AHcAhACOAPIA9wD/BGcEaQRuBHkEggSQBJQEmwSkBKkEtgS5BMsEzgTTAAAAAAAAAgEAAAAAAAAAKAAAAAAAAAAAAAAAAAAABNU=},
  Bdsk-Url-1 = {http://www.sciencedirect.com/science/article/B6VC8-4W7RK1H-1/2/6e0f4f827e068b51e213fb931cf73d38},
  Bdsk-Url-2 = {http://dx.doi.org/10.1016/j.ipm.2009.03.002}}

[3] E. Amigó, J. Gonzalo, J. Artiles, and F. Verdejo, “A comparison of extrinsic clustering evaluation metrics based on formal constraints,” Information Retrieval, vol. 12, iss. 4, pp. 461-486, 2009.
[Bibtex]

@article{ami:gon:art:ver:09,
  Author = {Amig{\'o}, E. and Gonzalo, J and Artiles, J. and Verdejo, F.},
  Date-Added = {2014-03-07 20:13:05 +0000},
  Date-Modified = {2014-03-07 20:13:20 +0000},
  Journal = {Information Retrieval},
  Number = {4},
  Pages = {461--486},
  Title = {{A comparison of extrinsic clustering evaluation metrics based on formal constraints}},
  Volume = {12},
  Year = {2009}}

[4] B. Mirkin, Mathematical Classification and Clustering, Kluwer Academic Publishers, 1996, vol. 11.
[Bibtex]

@book{mir:96,
  Author = {Boris Mirkin},
  Date-Added = {2014-03-10 16:07:22 +0000},
  Date-Modified = {2014-03-10 16:07:22 +0000},
  Keywords = {clustering classification biclustering},
  Publisher = {Kluwer Academic Publishers},
  Series = {Nonconvex Optimization and Its Applications},
  Title = {Mathematical Classification and Clustering},
  Volume = {11},
  Year = {1996}}

[5] N. Japkowicz and M. Shah, Evaluating Learning Algorithms: A Classification Perspective, Cambridge University Press, 2011.
[Bibtex]

@book{jap:sha:11,
  Author = {Japkowicz, Nathalie and Shah, Mohak},
  Date-Added = {2012-12-05 11:53:38 +0000},
  Date-Modified = {2012-12-05 11:54:26 +0000},
  Month = jan,
  Publisher = {Cambridge University Press},
  Title = {Evaluating Learning Algorithms: A Classification Perspective},
  Year = {2011}}

[6] T. Fawcett, “ROC Graphs: Notes and Practical Considerations for Researchers,” , 2004.
[Bibtex]

@article{Fawcett:2004p59,
  Abstract = {Receiver Operating Characteristics (ROC) graphs are a useful technique for organizing classifiers and visualizing their performance. ROC graphs are commonly used in medical decision making, and in recent years have been increasingly adopted in the machine learning and data mining research communities. Although ROC graphs are apparently simple, there are some common misconceptions and pitfalls when using them in practice. This article serves both as a tutorial introduction.
             },
  Affiliation = {HP Laboratories, MS 1143, 1501 Page Mil l Road, Palo Alto, CA 94304},
  Author = {Tom Fawcett},
  Date-Added = {2007-06-14 11:25:07 +0200},
  Date-Modified = {2010-04-19 12:58:13 +0200},
  Local-Url = {file://localhost/Users/fva/Documents/Papers/2004/Fawcett/Fawcett%202004%20ROC%20Graphs%20Notes%20and%20Practical.pdf},
  Month = {Jun},
  Rating = {5},
  Read = {Yes},
  Title = {ROC Graphs: Notes and Practical Considerations for Researchers},
  Uri = {papers://15492FEA-4C5B-4BEA-89B8-8663EEC734AB/Paper/p59},
  Year = {2004},
  Bdsk-File-1 = {YnBsaXN0MDDUAQIDBAUGJCVYJHZlcnNpb25YJG9iamVjdHNZJGFyY2hpdmVyVCR0b3ASAAGGoKgHCBMUFRYaIVUkbnVsbNMJCgsMDxJXTlMua2V5c1pOUy5vYmplY3RzViRjbGFzc6INDoACgAOiEBGABIAFgAdccmVsYXRpdmVQYXRoWWFsaWFzRGF0YV8QUy4uLy4uL0RvY3VtZW50cy9QYXBlcnMvMjAwNC9GYXdjZXR0L0Zhd2NldHQgMjAwNCBST0MgR3JhcGhzIE5vdGVzIGFuZCBQcmFjdGljYWwucGRm0hcLGBlXTlMuZGF0YU8RA04AAAAAA04AAgAAA2Z2YQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAMdNTldIKwAFAAJt6x9GYXdjZXR0IDIwMDQgUk9DIEdyYXAjMjZERUMucGRmAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAm3swuc/vVBERiBDQVJPAAIABQAADQIAAAAAAAAAAAAAAAAAAAAHRmF3Y2V0dAAAEAAIAADHTUBHAAAAEQAIAADC5yOdAAAAAQAQAAJt6wACbbkAAmqvAAJppgACAEFmdmE6RG9jdW1lbnRzOlBhcGVyczoyMDA0OkZhd2NldHQ6RmF3Y2V0dCAyMDA0IFJPQyBHcmFwIzI2REVDLnBkZgAADgBgAC8ARgBhAHcAYwBlAHQAdAAgADIAMAAwADQAIABSAE8AQwAgAEcAcgBhAHAAaABzACAATgBvAHQAZQBzACAAYQBuAGQAIABQAHIAYQBjAHQAaQBjAGEAbAAuAHAAZABmAA8ACAADAGYAdgBhABIATi9Eb2N1bWVudHMvUGFwZXJzLzIwMDQvRmF3Y2V0dC9GYXdjZXR0IDIwMDQgUk9DIEdyYXBocyBOb3RlcyBhbmQgUHJhY3RpY2FsLnBkZgATAAovVXNlcnMvZnZhABQBXAAAAAABXAACAAEMTWFjaW50b3NoIEhEAAAAAAAAAAAAAAAAAAAAxquYFkgrAAAAB/whEGZ2YS5zcGFyc2VidW5kbGUAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAH/CK2dYdYAAAAAAAAAAD/////AAAJIAAAAAAAAAAAAAAAAAAAAAQuZnZhABAACAAAxqt79gAAABEACAAAtnV5SAAAAAEACAAH/CEAAJDnAAIAKE1hY2ludG9zaCBIRDpVc2VyczouZnZhOmZ2YS5zcGFyc2VidW5kbGUADgAiABAAZgB2AGEALgBzAHAAYQByAHMAZQBiAHUAbgBkAGwAZQAPABoADABNAGEAYwBpAG4AdABvAHMAaAAgAEgARAASABtVc2Vycy8uZnZhL2Z2YS5zcGFyc2VidW5kbGUAABMAAS8A//8AAAAVAAIACv//AACABtIbHB0eWiRjbGFzc25hbWVYJGNsYXNzZXNdTlNNdXRhYmxlRGF0YaMdHyBWTlNEYXRhWE5TT2JqZWN00hscIiNcTlNEaWN0aW9uYXJ5oiIgXxAPTlNLZXllZEFyY2hpdmVy0SYnVHJvb3SAAQAIABEAGgAjAC0AMgA3AEAARgBNAFUAYABnAGoAbABuAHEAcwB1AHcAhACOAOQA6QDxBEMERQRKBFUEXgRsBHAEdwSABIUEkgSVBKcEqgSvAAAAAAAAAgEAAAAAAAAAKAAAAAAAAAAAAAAAAAAABLE=},
  Bdsk-Url-1 = {http://home.comcast.net/~tom.fawcett/public_html/papers/ROC101.pdf}}

[7]

A. P. Bradley, “The use of the area under the ROC curve in the evaluation of machine learning algorithms,” Pattern Recognition, vol. 30, iss. 7, pp. 1145-1159, 1997.
[Bibtex]

@article{bra:97,
  Author = {Andrew P. Bradley},
  Date-Added = {2014-03-07 20:08:15 +0000},
  Date-Modified = {2014-03-07 20:08:15 +0000},
  Doi = {DOI: 10.1016/S0031-3203(96)00142-2},
  Issn = {0031-3203},
  Journal = {Pattern Recognition},
  Keywords = {Standard error},
  Number = {7},
  Pages = {1145 - 1159},
  Title = {The use of the area under the {ROC} curve in the evaluation of machine learning algorithms},
  Volume = {30},
  Year = {1997},
  Bdsk-Url-1 = {http://www.sciencedirect.com/science/article/B6V14-3SNVHWM-R/2/c6e1fc455f5451480b9a3bd9985cfb6c},
  Bdsk-Url-2 = {http://dx.doi.org/10.1016/S0031-3203(96)00142-2}}

[8] X. Zhu and I. Davidson, Knowledge discovery and data mining: challenges and realities, Information Science Reference, 2007.
[Bibtex]

@book{zhu:dav:07,
  Author = {Zhu, X. and Davidson, I.},
  Date-Added = {2014-03-10 16:10:38 +0000},
  Date-Modified = {2014-03-10 16:13:13 +0000},
  Publisher = {Information Science Reference},
  Series = {Premier reference source},
  Title = {Knowledge discovery and data mining: challenges and realities},
  Year = {2007},
  Bdsk-Url-1 = {http://books.google.es/books?id=zdJQAAAAMAAJ}}

[9] A. Ben-David, “A lot of randomness is hiding in accuracy,” Engineering Applications of Artificial Intelligence, vol. 20, iss. 7, p. 875—885, 2007.
[Bibtex]

@article{dav:07,
  Abstract = {The proportion of successful hits, usually referred to as ``accuracy'', is by far the most dominant meter for measuring classifiers' accuracy. This is despite of the fact that accuracy does not compensate for hits that can be attributed to mere chance. Is it a meaningful flaw in the context of machine learning? Are we using the wrong meter for decades? The results of this study do suggest that the answers to these questions are positive.

Cohen's kappa, a meter that does compensate for random hits, was compared with accuracy, using a benchmark of fifteen datasets and five well-known classifiers. It turned out that the average probability of a hit being the result of mere chance exceeded one third (!). It was also found that the proportion of random hits varied with different classifiers that were applied even to a single dataset. Consequently, the rankings of classifiers' accuracy, with and without compensation for random hits, differed from each other in eight out of the fifteen datasets. Therefore, accuracy may well fail in its main task, namely to properly measure the accuracy-wise merits of the classifiers themselves.},
  Author = {Arie Ben-David},
  Date-Added = {2014-03-15 07:49:18 +0000},
  Date-Modified = {2014-03-15 07:49:18 +0000},
  Journal = {Engineering Applications of Artificial Intelligence},
  Local-Url = {file://localhost/Users/fva/Documents/Papers/2007/Ben-David/Ben-David%202007%20A%20lot%20of%20randomness%20is.pdf},
  Number = {7},
  Pages = {875---885},
  Rating = {0},
  Title = {A lot of randomness is hiding in accuracy},
  Uri = {papers://15492FEA-4C5B-4BEA-89B8-8663EEC734AB/Paper/p19681},
  Volume = {20},
  Year = {2007},
  Bdsk-File-1 = {YnBsaXN0MDDUAQIDBAUGJCVYJHZlcnNpb25YJG9iamVjdHNZJGFyY2hpdmVyVCR0b3ASAAGGoKgHCBMUFRYaIVUkbnVsbNMJCgsMDxJXTlMua2V5c1pOUy5vYmplY3RzViRjbGFzc6INDoACgAOiEBGABIAFgAdccmVsYXRpdmVQYXRoWWFsaWFzRGF0YV8QVS4uLy4uLy4uLy4uL0RvY3VtZW50cy9QYXBlcnMvMjAwNy9CZW4tRGF2aWQvQmVuLURhdmlkIDIwMDcgQSBsb3Qgb2YgcmFuZG9tbmVzcyBpcy5wZGbSFwsYGVdOUy5kYXRhTxEDQgAAAAADQgACAAADZnZhAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAx01OV0grAAUAAm9XH0Jlbi1EYXZpZCAyMDA3IEEgbG90IzM2MUMzMy5wZGYAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA2HDPHLIxCUERGIENBUk8ABAAFAAANAgAAAAAAAAAAAAAAAAAAAAlCZW4tRGF2aWQAABAACAAAx01ARwAAABEACAAAxyx+MgAAAAEAEAACb1cAAm88AAJqrwACaaYAAgBDZnZhOkRvY3VtZW50czpQYXBlcnM6MjAwNzpCZW4tRGF2aWQ6QmVuLURhdmlkIDIwMDcgQSBsb3QjMzYxQzMzLnBkZgAADgBUACkAQgBlAG4ALQBEAGEAdgBpAGQAIAAyADAAMAA3ACAAQQAgAGwAbwB0ACAAbwBmACAAcgBhAG4AZABvAG0AbgBlAHMAcwAgAGkAcwAuAHAAZABmAA8ACAADAGYAdgBhABIASi9Eb2N1bWVudHMvUGFwZXJzLzIwMDcvQmVuLURhdmlkL0Jlbi1EYXZpZCAyMDA3IEEgbG90IG9mIHJhbmRvbW5lc3MgaXMucGRmABMACi9Vc2Vycy9mdmEAFAFcAAAAAAFcAAIAAQxNYWNpbnRvc2ggSEQAAAAAAAAAAAAAAAAAAADGq5gWSCsAAAAH/CEQZnZhLnNwYXJzZWJ1bmRsZQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAf8IrZ1h1gAAAAAAAAAAP////8AAAkgAAAAAAAAAAAAAAAAAAAABC5mdmEAEAAIAADGq3v2AAAAEQAIAAC2dXlIAAAAAQAIAAf8IQAAkOcAAgAoTWFjaW50b3NoIEhEOlVzZXJzOi5mdmE6ZnZhLnNwYXJzZWJ1bmRsZQAOACIAEABmAHYAYQAuAHMAcABhAHIAcwBlAGIAdQBuAGQAbABlAA8AGgAMAE0AYQBjAGkAbgB0AG8AcwBoACAASABEABIAG1VzZXJzLy5mdmEvZnZhLnNwYXJzZWJ1bmRsZQAAEwABLwD//wAAABUAAgAK//8AAIAG0hscHR5aJGNsYXNzbmFtZVgkY2xhc3Nlc11OU011dGFibGVEYXRhox0fIFZOU0RhdGFYTlNPYmplY3TSGxwiI1xOU0RpY3Rpb25hcnmiIiBfEA9OU0tleWVkQXJjaGl2ZXLRJidUcm9vdIABAAgAEQAaACMALQAyADcAQABGAE0AVQBgAGcAagBsAG4AcQBzAHUAdwCEAI4A5gDrAPMEOQQ7BEAESwRUBGIEZgRtBHYEewSIBIsEnQSgBKUAAAAAAAACAQAAAAAAAAAoAAAAAAAAAAAAAAAAAAAEpw==},
  Bdsk-Url-1 = {http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6V2M-4N4406X-1&_user=143961&_origUdi=B6V14-3SNVHWM-R&_fmt=high&_coverDate=10%252F31%252F2007&_rdoc=1&_orig=article&_acct=C000011938&_version=1&_urlVersion=0&_userid=143961&md5=2a72374f1ddffe4d726cfceb1f9a72be}}

[10] M. Meila, “Comparing clusterings—an information based distance,” Journal of Multivariate Analysis, vol. 28, pp. 875-893, 2007.
[Bibtex]

@article{mei:07,
  Author = {Marina Meila},
  Date-Added = {2014-03-07 20:07:58 +0000},
  Date-Modified = {2014-03-07 20:07:58 +0000},
  Journal = {Journal of Multivariate Analysis},
  Local-Url = {file://localhost/Users/fva/Documents/Papers/2007/Meila/Meila%202007%20Comparing%20clusterings%E2%80%94an%20information%20based%20distance.pdf},
  Pages = {875--893},
  Pmid = {13462939817480528545related:oaJjLW_41boJ},
  Rating = {1},
  Title = {Comparing clusterings---an information based distance},
  Uri = {papers://15492FEA-4C5B-4BEA-89B8-8663EEC734AB/Paper/p18603},
  Volume = {28},
  Year = {2007},
  Bdsk-File-1 = {YnBsaXN0MDDUAQIDBAUGJCVYJHZlcnNpb25YJG9iamVjdHNZJGFyY2hpdmVyVCR0b3ASAAGGoKgHCBMUFRYaIVUkbnVsbNMJCgsMDxJXTlMua2V5c1pOUy5vYmplY3RzViRjbGFzc6INDoACgAOiEBGABIAFgAdccmVsYXRpdmVQYXRoWWFsaWFzRGF0YW8QagAuAC4ALwAuAC4ALwAuAC4ALwAuAC4ALwBEAG8AYwB1AG0AZQBuAHQAcwAvAFAAYQBwAGUAcgBzAC8AMgAwADAANwAvAE0AZQBpAGwAYQAvAE0AZQBpAGwAYQAgADIAMAAwADcAIABDAG8AbQBwAGEAcgBpAG4AZwAgAGMAbAB1AHMAdABlAHIAaQBuAGcAcyAUAGEAbgAgAGkAbgBmAG8AcgBtAGEAdABpAG8AbgAgAGIAYQBzAGUAZAAgAGQAaQBzAHQAYQBuAGMAZQAuAHAAZABm0hcLGBlXTlMuZGF0YU8RA4QAAAAAA4QAAgAAA2Z2YQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAMdNTldIKwAFAAJvtB9NZWlsYSAyMDA3IENvbXBhcmluZyMzNjFBOEUucGRmAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAANhqOyFucmVBERiBDQVJPAAQABQAADQIAAAAAAAAAAAAAAAAAAAAFTWVpbGEAABAACAAAx01ARwAAABEACAAAyFuAeQAAAAEAEAACb7QAAm88AAJqrwACaaYAAgA/ZnZhOkRvY3VtZW50czpQYXBlcnM6MjAwNzpNZWlsYTpNZWlsYSAyMDA3IENvbXBhcmluZyMzNjFBOEUucGRmAAAOAIYAQgBNAGUAaQBsAGEAIAAyADAAMAA3ACAAQwBvAG0AcABhAHIAaQBuAGcAIABjAGwAdQBzAHQAZQByAGkAbgBnAHMgFABhAG4AIABpAG4AZgBvAHIAbQBhAHQAaQBvAG4AIABiAGEAcwBlAGQAIABkAGkAcwB0AGEAbgBjAGUALgBwAGQAZgAPAAgAAwBmAHYAYQASAGEvRG9jdW1lbnRzL1BhcGVycy8yMDA3L01laWxhL01laWxhIDIwMDcgQ29tcGFyaW5nIGNsdXN0ZXJpbmdz4oCUYW4gaW5mb3JtYXRpb24gYmFzZWQgZGlzdGFuY2UucGRmAAATAAovVXNlcnMvZnZhABQBXAAAAAABXAACAAEMTWFjaW50b3NoIEhEAAAAAAAAAAAAAAAAAAAAxquYFkgrAAAAB/whEGZ2YS5zcGFyc2VidW5kbGUAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAH/CK2dYdYAAAAAAAAAAD/////AAAJIAAAAAAAAAAAAAAAAAAAAAQuZnZhABAACAAAxqt79gAAABEACAAAtnV5SAAAAAEACAAH/CEAAJDnAAIAKE1hY2ludG9zaCBIRDpVc2VyczouZnZhOmZ2YS5zcGFyc2VidW5kbGUADgAiABAAZgB2AGEALgBzAHAAYQByAHMAZQBiAHUAbgBkAGwAZQAPABoADABNAGEAYwBpAG4AdABvAHMAaAAgAEgARAASABtVc2Vycy8uZnZhL2Z2YS5zcGFyc2VidW5kbGUAABMAAS8A//8AAAAVAAIACv//AACABtIbHB0eWiRjbGFzc25hbWVYJGNsYXNzZXNdTlNNdXRhYmxlRGF0YaMdHyBWTlNEYXRhWE5TT2JqZWN00hscIiNcTlNEaWN0aW9uYXJ5oiIgXxAPTlNLZXllZEFyY2hpdmVy0SYnVHJvb3SAAQAIABEAGgAjAC0AMgA3AEAARgBNAFUAYABnAGoAbABuAHEAcwB1AHcAhACOAWUBagFyBPoE/AUBBQwFFQUjBScFLgU3BTwFSQVMBV4FYQVmAAAAAAAAAgEAAAAAAAAAKAAAAAAAAAAAAAAAAAAABWg=},
  Bdsk-Url-1 = {http://linkinghub.elsevier.com/retrieve/pii/S0047259X06002016}}

[11] R. M. Fano, Transmission of Information: A Statistical Theory of Communication, The MIT Press, 1961.
[Bibtex]

@book{fan:61,
  Abstract = {A basic text on the theoretical foundations of information theory, for graduate students and engineers interested in electrical communications and for others },
  Author = {Robert M. Fano},
  Date-Added = {2014-03-07 14:33:46 +0000},
  Date-Modified = {2014-03-07 14:33:46 +0000},
  Pages = {400},
  Pmid = {vIlKQgAACAAJ},
  Publisher = {The MIT Press},
  Rating = {0},
  Title = {Transmission of Information: A Statistical Theory of Communication},
  Year = {1961},
  Bdsk-Url-1 = {http://books.google.com/books?id=vIlKQgAACAAJ&printsec=frontcover}}

[12] Francisco~J.~Valverde-Albacete and C. Peláez-Moreno, “Two information-theoretic tools to assess the performance of multi-class classifiers,” Pattern Recognition Letters, vol. 31, iss. 12, pp. 1665-1671, 2010.
[Bibtex]

@article{val:pel:10b,
  Annote = {doi:10.1016/j.patrec.2010.05.017},
  Author = {Francisco~J.~Valverde-Albacete and Carmen Pel\'aez-Moreno},
  Date-Added = {2014-03-10 16:29:39 +0000},
  Date-Modified = {2014-03-10 16:29:39 +0000},
  Journal = {Pattern Recognition Letters},
  Number = {12},
  Pages = {1665--1671},
  Title = {Two information-theoretic tools to assess the performance of multi-class classifiers},
  Volume = {31},
  Year = {2010}}

[13] R. Shwartz-Ziv and N. Tishby, “Opening the Black Box of Deep Neural Networks via Information.,” CoRR, 2017.
[Bibtex]

@article{sch:tis:17,
  Author = {Shwartz-Ziv, Ravid and Tishby, Naftali},
  Date-Added = {2017-12-15 17:45:46 +0000},
  Date-Modified = {2017-12-15 17:45:46 +0000},
  Journal = {CoRR},
  Title = {{Opening the Black Box of Deep Neural Networks via Information.}},
  Year = {2017}}

[14] N. Tishby and N. Zaslavsky, “Deep Learning and the Information Bottleneck Principle.,” in IEEE 2015 Information Theory Workshop, 2015.
[Bibtex]

@inproceedings{tis:zas:15,
  Author = {Tishby, Naftali and Zaslavsky, Noga},
  Booktitle = {IEEE 2015 Information Theory Workshop},
  Date-Added = {2017-12-15 17:45:46 +0000},
  Date-Modified = {2017-12-15 17:45:46 +0000},
  Title = {{Deep Learning and the Information Bottleneck Principle.}},
  Year = {2015}}

IJCNN 2018 Tutorial

Entropic Evaluation of Classification A hands-on, get-dirty introduction